Singular Value Decomposition Demo
This is a quick demo of what Singular Value Decomposition does. The math is based on notes from Data Mining and Engineering.
Math
Starting with data \( X \) of size \( D \times N \), which represents \( N \) examples of \( D \)-dimensional data, if I run SVD on it and ask for \( K \) dimensions, SVD will decompose it into
where \( S \) is a diagonal matrix of size \( K \times K \), \( U \) and \( V \) are orthonormal matrices, and if \( X \) of size \( D \times N \), then \( U \) is size \( D \times K \) and \( V \) is of size \( K \times N \).
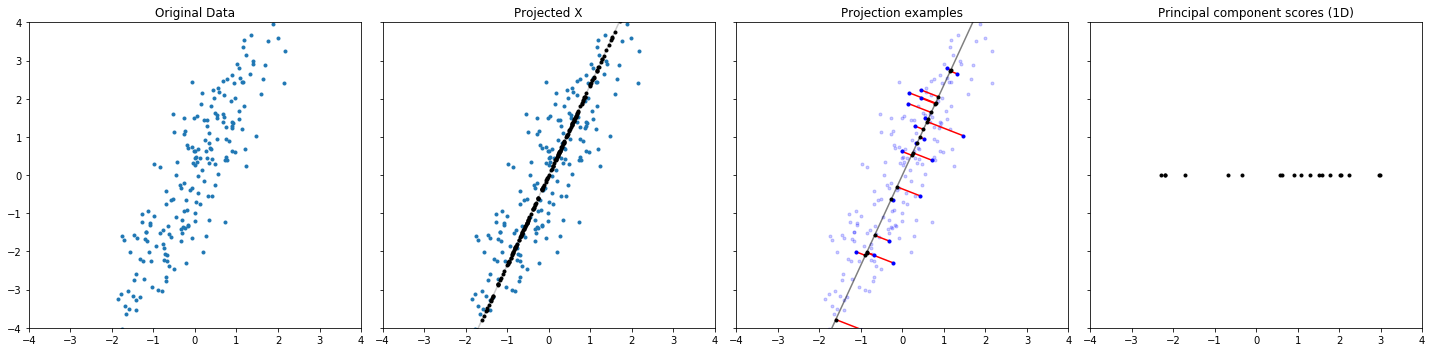
# Generate data!
D = 2
N = 200
L = np.tril(np.ones((D, D)))
x = np.vstack(((1, 0), (2, 1))) @ np.random.randn(D, N)
# SVD!
k = 1
u, s, vt = svds(x, k=k)
print(s)
print('k =', k, ', x shape', x.shape, ', u shape', u.shape, ', s shape', s.shape, ', vt shape', vt.shape)
# Projecting!
projected_x = u @ u.T @ x
# principle component direction
principle_component_direction_line = u @ np.linspace(-10, 10, 100).reshape(1, -1)
print('principle component direction\n', u)
# first principle component scores
principle_component_score = s @ vtPlotting