This is another thing I learned while implementing convolutions for a convolutional neural net. See part 1 for the motivation.

  • Part 1 is an introduction to the problem and how I used numpy.lib.stride_tricks.as_strided.
  • Part 2 is about numpy.einsum.

What now?

After using as_strided, I have a 4D representation of the image like this:

Strided

and I need to multiply each of those 3 x 3 matrices by its corresponding value in the kernel

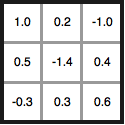
Kernel params

and sum over those 9 values to create the value in the feature map.

Einsum

One way is to use numpy.tensordot. But there’s another tool: numpy.einsum.

When I was looking at StackOverflow for direction, a lot of them used numpy.einsum. It took me a while to look into it because it looked cryptic.

This blog about einsum helped me first understand it. I recommend it! The docs also help once I got a few examples working.

Matrix Multiplication

np.einsum looks pretty scary. Matrix multiplication becomes:

np.einsum('ij,jk->ik', A, B)

ij,jk->ik, or the “einstein sum subscripts string,” tells einsum what it should do. The groups of letters are the operands and represent the arrays it should act on.

ij,jk->ik is defining a little function array1, array2 -> output.

Each letter labels an axis. ij is labeling the two axes of A.

I can read ij,jk->ik as “takes a 2D matrix, another 2D matrix, and returns a third 2D matrix.”

Then there are the rules:

  • repeating a letter on the left-hand side of the arrow means to multiply along those axes
  • omitting a letter from the right-hand side means sum over this axis.
  • the order of the letters in the output is the order of the array, so I can transpose too.

This example

tbh, what ended up working best was not thinking too hard, labeling my input axes and my output axes and following the rules to update it.

In this case, I wanted to multiply the last two dimensions of the expanded_inputs by its corresponding value in the kernel. So xyij,ij will do that because ij is in the expanded_inputs and kernel. The result should be of size xy. This gives me the function

feature_map = np.einsum(
    'xyij,ij->xy',
    expanded_input,
    kernel,
)

Higher dimensional tensors are no big deal

I actually needed to do this with even larger tensors, with dimensions for the items in a minibatch, the number of input feature maps, and output feature maps. Labeling the dimensions and following the rules made this a little less of a headache. For example, getting gradients during back propagation looked something like this:

# n - N
# i - inputs
# o - outputs
# x - feature map dim1
# y - feature map dim2
# i - kernel dim1
# j - kernel dim2
conved = np.einsum(
    'nijkde,node->oijk',
    conv_view,
    grads_wrt_outputs,
)

See Also